日前，伟德bevictor中文版官网数学与统计学院朱蓉禅副教授在国际顶级学术期刊《The annals of Probability》上发表了题为《Lattice approximation to the dynamical 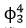 model》的研究论文。该研究构造了以格点上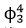场的逼近测度为不变分布的有限维系统收敛到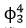动力模型。 这对应于量子场论中重要的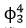场格点逼近，由此可以得到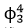动力模型以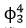场为不变测度。

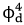　　动力模型是对量子场论中基本模型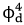场提出的随机量子化模型，即构造一个随机偏微分方程即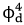动力模型使得当时间趋于无穷时方程的解依分布收敛到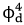场。由此运用随机分析的方法研究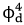场。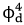动力模型是一类带有奇异噪声的随机偏微分方程，如何在d="3时给出方程解的适定性是公开了很多年的问题。2011年英国帝国理工大学的Hairer教授在中用粗糙路径理论处理方程解在一维空间的奇异性,并以此构造了一维KPZ方程的解。之后，Hairer教授结合泰勒展开的思想提出了一套新理论：正则结构理论(regularity" structure)，给出了次临界条件下证明带有奇异噪声的随机偏微分方程局部适定性的一般方法，这是随机偏微分方程领域的重大发展。由此证明了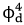动力模型局部适定性。Haire教授因此获得了2014年Fields奖。同时，Gubinelli-Imkeller-Perkowski基于被控制的粗糙路径(controlled rough path)和调和分析中的仿积提出了拟控制分布(paracontrolled distribution)的方法。这个方法也可以用来研究奇异的随机偏微分方程。Gubinelli教授也因此受邀在2018年国际数学家大会作45分钟报告。目前，这两套方法是随机分析领域的重大发展。

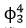　　场的格点逼近是研究和构造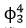场的一种重要方法，它保持了测度的铁磁本质和Osterwalder–Schrader公理。朱蓉禅副教授在上诉论文中运用拟控制分布首先研究了以格点上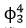场的逼近测度为不变分布的有限维系统。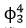动力模型可以看成是三维环面上的模型，因此要证明收敛性需要将格点系统模型延拓到环面上进行比较。这时延拓时会产生有限维投影算子，这个算子会导致拟控制分布中非常本质的交换子估计不成立，分析方法无法运用。这时朱蓉禅副教授及合作者在论文中将投影算子中余项部分运用概率计算的方法证明了收敛。

　　这一结果进一步增进了人们对于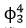场动力系统及其格点逼近之间的关系。既可以用来联系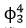场和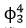动力模型，也可以用来构造与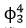场对应的狄氏型，由此回答了以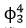场为参考测度的二次型可闭的公开问题。

　　该研究工作由朱蓉禅副教授和北京交通大学朱湘禅副教授合作完成。朱蓉禅副教授为本文的第一作者。本工作得到国家自然科学基金的支持。

　　论文链接地址：https://projecteuclid.org/euclid.aop/1517821226

【课题组及负责人简介】

　　伟德bevictor中文版官网数学与统计学院概率团队积极开展实质性国际合作研究，团队成员积极开展国际学术交流。

　　朱蓉禅，副教授，硕士生导师，本科毕业于四川大学、博士是中科院数学与系统科学研究院与德国比勒菲尔德大学联合培养。德国比勒菲尔德大学访问学者。长期从事随机偏微分方程、狄氏型、随机分析的研究工作，先后主持/完成了国家自然科学基金面上项目、青年项目。以第一/通讯作者在The annals of probability、Communication in mathematical physics、Journal of functional analysis、Journal of differential equaitons等期刊发表SCI论文20余篇。